İçindekiler [göster]
Suya çelik bir çiviyi düşürdüğünüzde neden bir taş gibi battığını merak ettiniz mi? Fakat iyi inşa edilmiş çelik bir gemi okyanusta olduğunda, küçük bir çiviye göre çok daha ağır olmasına rağmen yüzüyor? Gemiler neden batmaz ancak taş batar?
Archimedes’in Yüzdürme Prensibi
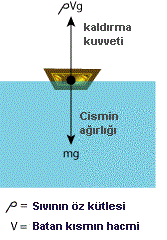
MÖ 3. yüzyılda yaşamış olan Yunan matematikçi ve fizikçi Archimedes, suya batırılan bir cismin, batırıldığı suyun hacmi kadar suyu displase ettiğini, yani kenara ittiğini keşfetti. Ayrıca bu cismin üzerinde, ittiği suyun ağırlığına eşit bir kuvvetin yukarı doğru uygulandığını fark etti. Bu kuvvete “yüzdürme kuvveti” denir ve bir cismin su üzerinde kalıp kalmayacağını belirleyen temel faktördür.
Gemiler, çelik gibi yoğun malzemelerden yapılmasına rağmen, içlerinde hava bulunduracak şekilde tasarlanmıştır. Bu tasarım, geminin toplam yoğunluğunun, suyun yoğunluğundan daha düşük olmasını sağlar. Böylece gemi, üzerinde taşıdığı ağırlığa rağmen su üzerinde yüzebilir.
Gemilerin Tasarımı ve Yüzme Kabiliyeti
Bir geminin yüzebilmesi için, suya batırıldığında displase ettiği su miktarının ağırlığının, geminin kendi ağırlığından fazla olması gerekmektedir. Modern gemi mühendisliği, geminin yüzeyini geniş ve boşluklu yaparak, geminin displase ettiği su miktarını maksimize etmeye çalışır. Geminin gövdesi, hem yeterince geniş hacim yaratmak hem de yüzdürme kuvvetini artırmak için özel olarak şekillendirilir.
Gemi gövdesinin alt kısmı, yani su ile temas eden kısım, genellikle düz veya hafif eğimli olup, suyun kolayca ayrılmasını ve geminin dengede kalmasını sağlar. Gemi yüzdükçe, suyun itme kuvveti geminin ağırlığına karşı gelir ve onu yüzdürür. Bu durumda, gemi ne kadar yük taşırsa taşısın, yeterince displase edilmiş su varsa batmaz.
Gemilerin Batmaması için Dikkat Edilmesi Gerekenler
Geminin batmaması için, yük dağılımının dengeli olması şarttır. Eğer gemi bir tarafına aşırı yüklenirse, yani asimetrik bir yük dağılımı olursa, yeterli yüzdürme kuvveti üretemeyebilir ve batma riski artar. Gemi inşaatçıları, bu dengenin korunmasına özellikle dikkat ederler.
Bir diğer önemli faktör ise geminin gövdesinin bütünlüğüdür. Gemi gövdesindeki herhangi bir delik veya çatlak, suyun gemi içine girmesine ve yüzdürme kuvvetinin azalmasına sebep olabilir. Bu nedenle, gemilerin düzenli olarak bakımının yapılması ve gövdenin sağlam tutulması hayati önem taşır
Konuyu daha iyi anlayabilmek için basit kaldırma kuvveti deneyi ile gözlemleyebiliriz.
Malzemeler
• Bez havlu (veya kağıt havlu)
• Büyük, açık kase veya kap
• Su
• Aliminyum folyo
• Metrik cetvel
• Dolma kalem
• Makas
• Tükenmez kalem
• Çekiç veya palet
Hazırlık
• Havluyu veya kağıt havluları sert bir yüzeye serin. Kasenin veya kabın içerisine üçte ikisini dolduracak şekilde musluk suyu koyun.
• Yaklaşık 25 santimetre (cm) karelik bir alüminyum folyo kare ölçün. Kareyi kesin. Bu, test ettiğiniz metal “tekne” haline gelecektir.
• Kalıcı işaretli kalem ile alüminyum folyonun dört köşesini işaretleyin.
• Dikkatli olun: Daha sonra deneyde çekiç kullanacaksınız. Kuvvetin dayanabileceği ve hasar görmeye karşı dayanıklı bir yüzey üzerinde işlemi yaptığınıza emin olun.
Prosedür
• Alüminyum folyonun kare köşelerini birlikte çekin ve kare yaklaşık altı cm çapında gevşek bir top haline getirin. İşaretli köşelerin bir arada kalması ve bir noktada görünmesini sağlayın.
• Topu hafifçe su haznesine yerleştirin, işaretli köşeleri topun üstünde olacak şekilde yerleştirin; bu, topun suyla dolmasını önlemeye yardımcı olur. Hemen topa dikkat et. Batıyor veya yüzüyor mu?
• Alüminyum folyo topu göz hizasında olması için alçaltın ve topun su yüzeyinin altındaki yüzeyinin ne kadar olduğuna dikkat edin. Sualtındaki kısmı topun yüzde 10, yüzde 25, yüzde 33, yüzde 50, yüzde 67, yüzde 75, yüzde 90 veya yüzde 100’ü var mı?
• Topu kaseden çıkarın, suyunu sallayın ve havlu üzerine kurutun.
• Şimdi topu yaklaşık 5 cm çaplı bir yere biraz sıkıştırın. Eğer çok fazla buruşursanız, istenen ebatları elde etmek için alüminyum folyodan bazılarını dikkatlice ayırın.
• Yine, işaretli köşeleri üste yerleştirerek topu nazikçe suyun içine koyun. Batıyor veya yüzüyor mu? Topun yüzde kaçı suyun üstündedir? Çıkarın, topu kurutun.
• Daha küçük ve daha sıkı olacak şekilde topu parçalamaya devam edin ve (yaptığınız gibi) yüzüp yüzmediğini test edin. Top tamamen tükenene kadar daha küçük çapları test etmeye devam edin. Bu çapları (veya kabaca benzer olanları) test etmeyi deneyin: 4,0 cm, 3,0 cm, 2,5 cm, 2,2 cm, 2,0 cm, 1,8 cm, 1,6 cm. Yalnızca el kuvveti ile topu sıkmak çok zorsa, folyoyu daha küçük bir topa hafifçe vurmak için çekiç veya paletle dikkatli bir şekilde kullanın (veya bunu yapabildiğinize göre bir top şekline yakın olarak). Test ettiğiniz her çap için topun yüzde kaçı batmış?
• Top hangi çapta tabana battı? Topun en düşük veya en yoğunluğa sahip olduğu çapları bulabilir misiniz? Top hangi çapta yaklaşık su yoğunluğuna eşit bir yoğunluğa sahipti? (Top neredeyse tamamen batırılmış veya tamamen suya batmıştı, ancak kabın tabanına tamamen batmadı mı?)
• Ekstra: 25 cm kare olan en az iki ilave alüminyum folyo sacını kesin ve bu işlemi tekrarlayın. Test ettiğiniz tüm alüminyum karelerle aynı sonuçları alıyor musunuz yoksa çok fazla varyasyon var mı?
• Ekstra: Bu aktiviteyi tekrar yapabilirsiniz, ancak bu sefer alüminyum tabakayı bir ölçekte tartıp gram cinsinden kütlesi hesaplayabilirsiniz. Bir kürenin hacminin, yarıçapının küpünün pi (3.14) katının dörtte üç misline eşit olması gerçeğini kullanarak, her bir çap için küre hacmini hesaplayın.
V=3/4×3,14xr^3
Kütle ve hacimleri kullanarak, kütleyi hacme bölürek her bir çap alüminyum levhanın ortalama yoğunluğunu hesaplayın. Alüminyum bilya hangi yoğunlukta battı? Alüminyum top yaklaşık olarak hangi yoğunluğa eşitti? Kürenin her çapı için yerinden edilen su kütlesi nedir? Daha doğru sonuçlar için ek 25 cm alüminyum kareleri test etmeye devam edin.
Gözlemler ve sonuçlar
Topun çapı azaldığında topun suyun altına gelen kısmında nasıl bir değişim yaşandı? Top yaklaşık 2,5 cm çapında iken su altındaki kısmı topun yarısı kadar olup, çapı yaklaşık 1,6 cm veya daha küçük olduğunda top tamamiyle gömüldü mü?
Bir nesne suya dalıyorsa, yerinden çıkmış su miktarı nesne ile aynı ağırlığa sahiptir. Dolayısıyla, yüzerken, topun çapı azaldığında aynı miktarda su yerinden çıkarmış olamıyordu ve bu nedenle kaldırma kuvveti aynı kalmadı. Bununla birlikte, topun yoğunluğu değişiyordu-topun çapı azaldığında yoğunluğu arttı.
Yoğunluk, birim hacim başına kütle-bir hacmine ne kadar “malzeme” konduğunu açıklar. Alüminyum bilye 6.0 cm’lik bir çapa sahip olduğunda, topun içindeki hava içerdiği için suyun yoğunluğundan daha düşük bir yoğunluğa sahip olduğu için topun iyi yüzmesi gerekir; tıpkı yüzen uçabilen çelik gemiler gibi yoğunlukları düşürüldü. Gövde içindeki havayı sarmalamaktadır. Ve gemi güçlü bir kaldırma kuvveti oluşturmak için yeterince su yer değiştirdiği müddetçe, kargo ile yüklü olsa bile, suyun üzerinde kalabilir. Çapı düştükçe ve yoğunluk arttıkça, top dahada batmaya başladı. Çapı yaklaşık 1,8 cm veya 1,6 cm olduğunda, yüzde 90 oranında (ancak zar zor) batmış olduğunu görmüş olabilirsiniz. Bu, top suyunkine yaklaşık bir yoğunluğa sahip olduğu zamandır. Yaklaşık 1,6 cm veya daha küçük bir çapa sahip topun tamamen batması gerekir; bu, yoğunluğunun suyunkinden büyük olduğunu ve dolayısıyla yüzen kuvvetin üstesinden geldiğini gösterir.